Temperature Dependence of a Lattice Constant

Introduction

Using X-ray diffraction, it is possible to identify crystal phases based on the crystalline structure of a material, and evaluate factors such as lattice length, and atom coordinate positions. Therefore, X-ray diffractometry is an analytic technique, which is essential for research on the properties of materials. Within diffractometry, X-ray diffraction measurement under high temperatures is a powerful technique, which goes beyond the identification of material structure and properties that are achieved with ordinary measurement. It enables examination of phase transitions and chemical reactions, which occur under high temperatures, deterioration conditions and synthesis processes, and temperature dependence of lattice constants.

Measurements and results

Temperature dependence of the lattice constant was evaluated for (La₀.₉,Sr₀.₁)MnO₃, an electrode material for solid oxide fuel cells. Under high temperatures, disturbance in the surface form of the sample occurs together with thermal expansion. Accurate diffraction angles were calculated using a parallel beam optical system in order to eliminate any affects from the surface form of the sample. In addition, measurement under high-temperatures was conducted using the Reactor-X infrared heating high-temperature attachment in order to maintain a stable temperature and measurement atmosphere. This measurement was conducted in the air. Figure 1 shows the X-ray diffraction patterns and qualitative analysis results at 27, 400, 600, 800, 900 and 1000°C. As a result of measurement, it was found that, from 27°C to 1000°C, (La₀.₉,Sr₀.₁)MnO₃ (hexagonal R3c) has a single phase, and there are no phase-changes at these temperatures.

Next, the lattice constant at each temperature was calculated using Rietveld analysis. As shown in Figure 2, it was found that the c-axis expands almost linearly with respect to the temperature rise; and that the a-axis exhibits a change in expansion coefficient starting around 800°C, with different coefficients on each side of this temperature boundary. In this way, it is possible to calculate an accurate lattice constant at each temperature by using a parallel beam optical system and an infrared heating high-temperature attachment. The measurement atmosphere in this case is the air, but with the infrared heating high-temperature attachment, the sample part and heater part are separated, so measurement can also be done in atmospheres of various gases such as H₂.

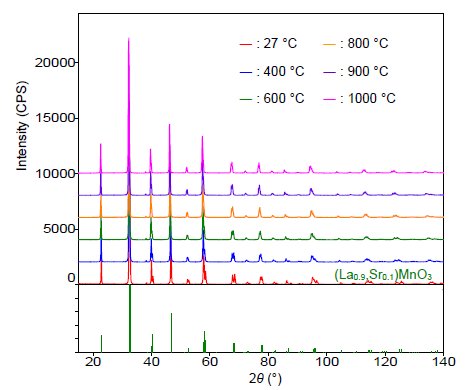Figure 1: X-ray diffraction patterns and qualitative analysis results for (La₀.₉,Sr₀.₁)MnO₃ at each temperature (Intensity is indicated with an offset)

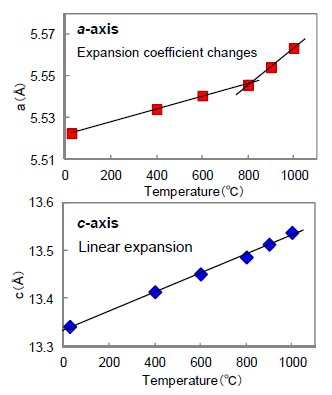
Figure 2: Temperature dependence of the lattice constants of (La₀.₉,Sr₀.₁)MnO₃