アプリケーション

 以前から第1ピーク未満 (短距離)の$G(r)$の傾きはサンプルの真密度に関連することが知られていましたが、第1ピークよりも短距離側では、$S(Q)$に含まれるにモジュレーションによるリップルが観測されるため傾きからでは精確な密度を算出することができませんでした。 そこで、$S(Q)$に含まれるモジュレーションを補正し、$G(r)$のリップルを抑制することによってサンプルの密度を求めることができるようになりました。

 SiO₂ガラスの密度を全散乱データから推定した例を紹介します。図に示すのは、密度推定過程における推定密度 ρ0 と推定密度との一致度 R の変化です。 繰り返し補正することにより推定密度が一定値に近づき残差は次第に小さくなっていることが分かります。 最終的に得られた密度の値は ρ₀=0.06311 atoms⋅Å⁻³ となり，報告されているSiO₂ガラスの密度 ^{1, 2)} (ρ_bulk=0.06613 atoms⋅Å⁻³) と比較すると5 %未満で一致しました。

SiO₂ガラスの密度推定時のイテレーション変化

 次にNiの全散乱データから密度を推定したところρ₀=0.09148 atoms⋅Å⁻³ となりました。この値は格子定数から求めた密度 ρ_bulk=0.09132 atoms⋅Å⁻³ と非常によく一致しています。 下の図に示したのは、補正前後でのS(Q) とG(r) の比較図です。補正前後で S(Q) と G(r) は大きく変化していないことが分かります。

補正前後の$S(Q)(左)$と$G(r)$(右)の比較図

 全散乱データによる密度推定法を用いることで、従来の密度計測法では測定困難なサンプル(禁水性のサンプルや構造中に細孔が存在する多孔質性のサンプルなど)の密度を計測することができるようになりました。
詳細な解説や解析例は文献を参考してください。

参考文献：

 正極材としてよく知られているスピネル型のマンガン酸リチウム ($\mathrm{LiMn_{2}O_{4}}$ LMO)は、室温付近で構造相転移することが知られています ^{1, 2)}。 高温相のLMO(下図 左)は、立方晶(cubic)の構造であり構造内は単一の$\mathrm{MnO_{6}}$八面体であることが知られています。 一方、低温相のLMO(下図 右)は、cubic型が$3a \times 3a \times 1a$で拡張された直方晶(Orthorhombic)で、$\mathrm{MnO_{6}}$八面体は5種類(各サイトで異なる構造)であることが知られています。 このようにユニークな特徴を持つLMOの局所構造をRMC法により解析した例を紹介します。

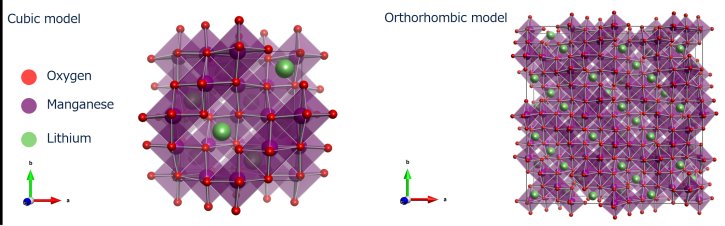
高温相と低温相のLMOの構造モデル図

 下図に示すのは、LMOの実測値と計算値の構造因子 $S(Q)$の比較です。また、下側のプロットは実測値と計算値の残差を示しています。
RMC法を使って推定したLMOの構造モデルは実測値を良く再現していることが分かります。

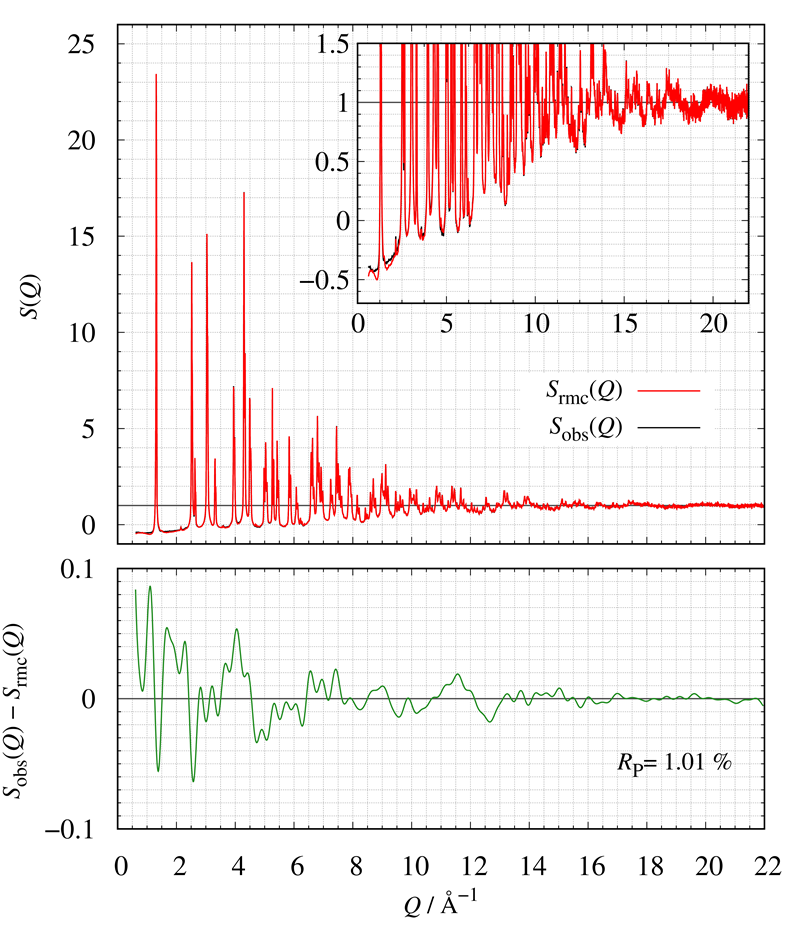
LMOの実測した$S(Q)$と計算した$S(Q)$の比較

 詳細なMnの特徴量を計算するために、LMOの構造中のMn原子の価数をBVS法により算出したところ (使用したBVSパラメーター: $r_0 = 1.753 Å$，$R=0.37 Å$)、 ほとんどのMnは3価 $(58.98 \%)$ と4価$(34.96 \%)$ に分類され、残りは2価 $(5.95 \%)$ と5価 $(0.097 \%)$ に分類されました。
2価と5価の割合は低いため、これ以降の解析では取り扱いません。下図に3価と4価のO-Mn-Oの角度ヒストグラムを示します。
3価の角度ヒストグラム(青実線)は、$\theta=90^{\circ}$付近に分布が2つありますが、4価の角度ヒストグラム(赤実線)では、$\theta=90^{\circ}$付近の分布は1つになっていることが分かります。
3価と4価の角度ヒストグラムの違いは、Jahn-Teller 効果によって引き起こされていると予測されます。本解析の詳細な説明は参考文献3, 4を参照してください。

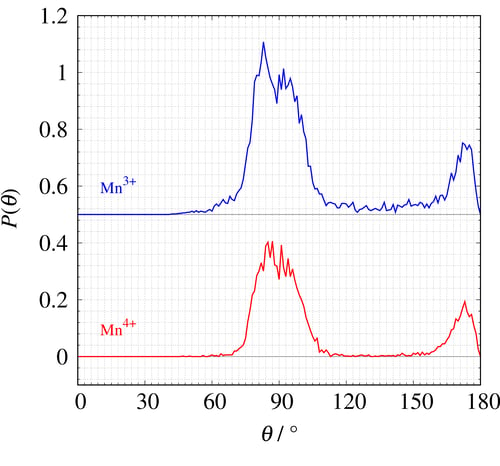
価数別のO-(Mn)-Oの角度ヒストグラム

 このように、RMC法を使うことで粉末構造解析ではできなかった詳細な局所構造の解析が実施できるようになりました。

参考文献：

　硫化物系固体電解質であるLi₃PS₄は複数の相を取りガラス相、γ相、β相とα相が知られています。3つの結晶相の特徴を図に示します。

各相の結晶構造の違いと相転移温度¹⁾

　このアプリケーションでは、室温から250℃の昇温過程で全散乱測定を実施しRMC法を使って結晶化過程の局所構造の変化を可視化しました。

　下図は、実測のG(r)と結晶状態(T = 250 °C,t = 75.5 h)の部分相関を比較したものです。r≥4.5 Åに現れるショルダーとピークはそれぞれP-S相関とS-S相関であることが分かります。結晶化に伴う実測のG(r)の違いがどの部分相関の影響なのかを調べることができます。

G(r)とw_ij G_ij (r)の比較
上: 各測定時間のG(r)、下: P-S、S-S、S-Liのw_ij G_ij (r)

　下図にRMC法で得られた原子座標を単位格子に戻した原子座標を示します。一般的な傾向として、ガラスから結晶になるに従い原子の分布が狭くなっています。しかし、詳細に解析してみると、高温のガラス状態の方が室温のガラス状態と比較して僅かに原子の分布が広くなっていました。単位格子内の原子分布の解析結果傾向は、先行研究のLiイオン伝導度の結果2)と一致していました。本研究により、PS₄アニオンの配置の乱れがLiイオンの伝導性に影響を与えていることが実験的に明らかになりました。

各測定温度における単位格子内の原子の分布の様子

本アプリケーションは参考文献3に詳細に記されています。

参考文献：