
PDF analysis has been attracting a lot of attention
Why not take structure analysis one step further?
Click on the tabs below to explore these topics:
Basic information about PDF analysis
The PDF (Pair Distribution Function) can extract information about interatomic distances and coordination numbers from scattering patterns independent of the crystallinity of the material.
The RDF (Radial Distribution Function) may be more familiar to some. It is essentially the same analysis with a different definition of the vertical axis.
Before we get into the explanation of PDF analysis, let's look at an example measurement using the X-ray scattering patterns of crystalline and amorphous carbon shown in Figure 1.

Figure 1. X-ray total scattering profiles of crystalline and amorphous carbon
(Courtesy of Dr. Kubota, Komaba Laboratory, Tokyo University of Science. Currently, his affiliation is NIMS. Learn more)
X-ray scattering patterns of amorphous carbon show broad peaks compared to the diffraction pattern of crystalline carbon. This happens because C-C bonds of various distances exist in the sample (microscopic view at the atomic bond scale), and scattered X-rays corresponding to each bonding distance interfere with each other. Therefore, the obtained scattering pattern can be Fourier transformed to directly obtain real-space information.
The obtained real-space information can be expressed in terms of coordination number or existence probability on the vertical axis and interatomic distance “r” on the horizontal axis. The profile plotted with RDF (coordination number) on the vertical axis and interatomic distance on the horizontal axis, and the structural model of carbon considered as a plane are shown in Figure 2.

Figure 2. Left: RDF of amorphous carbon; Right: Structure of carbon considered as a plane.
The peak position is related to the average interatomic distance and the peak area to the coordination number. Considering the 2D carbon structural model of carbon as a plane (in reality, information in 3-dimensional space is derived), each peak position indicated the 1st, 2nd, 3rd, $\cdots$ etc. neighbor distances.
This property makes it applicable to short-range structural analysis of amorphous systems and local structural disorder analysis of crystalline systems, and it is expected to be a promising method in a variety of fields.
Next, we will explain the PDF calculation method in more detail. Please refer to the Rigaku Journal1) and books for detailed formulas.
The following is a flow chart of the PDF calculation method:
①. Profile measurement (total scattering measurement)②. Calculation of structure factor $S(Q)$
③. Calculation PDF $G(r)$ by Fourier transform $S(Q)$
The points to keep in mind when measuring profiles are summarized in the section on total scattering measurement.
The structure factor $S(Q)$ is calculated from the following equation.
\begin{equation} S(Q) = \frac{I_{\mathrm{coh}} - \langle f^{2} \rangle + \langle f \rangle^{2}}{\langle f \rangle^{2}} \nonumber \end{equation} \begin{eqnarray} \langle f \rangle &= \sum_{i}^{n} c_{i}f_{i} \nonumber \\ \langle f^{2} \rangle &= \sum_{i}^{n} c_{i}f_{i}^{2} \nonumber \end{eqnarray}
where $c_{i}$ and $f_{i}$ are the concentration and atomic scattering factor of the $i$-th element and $I_{\mathrm{coh}}$ is the coherent scattering intensity derived from the sample structure extracted from the total X-ray scattering measurement data. To derive the coherent scattering, various corrections are applied to the obtained profile. Specifically, after background subtraction, polarization correction, absorption correction, and the Compton scattering correction, the experimentally profile is normalized by the atomic scattering factor.
PDF $G(r)$ can be obtained from the Fourier transform of the measured structure factor $S(Q)$.
Using $\mathrm {SiO}_{2}$ glass as an example, we show the definition equations2) and figures for four typical functions. The dashed line in each figure shows the average density in the system.
Reduced Pair Distribution Function $G(r)$
\begin{equation} G(r) = \frac{2}{\pi} \int^{Q_{\max}}_{Q_{\min}} {Q\{S(Q)-1\}\sin Qr} \,\mathrm{d}Q\nonumber \end{equation}
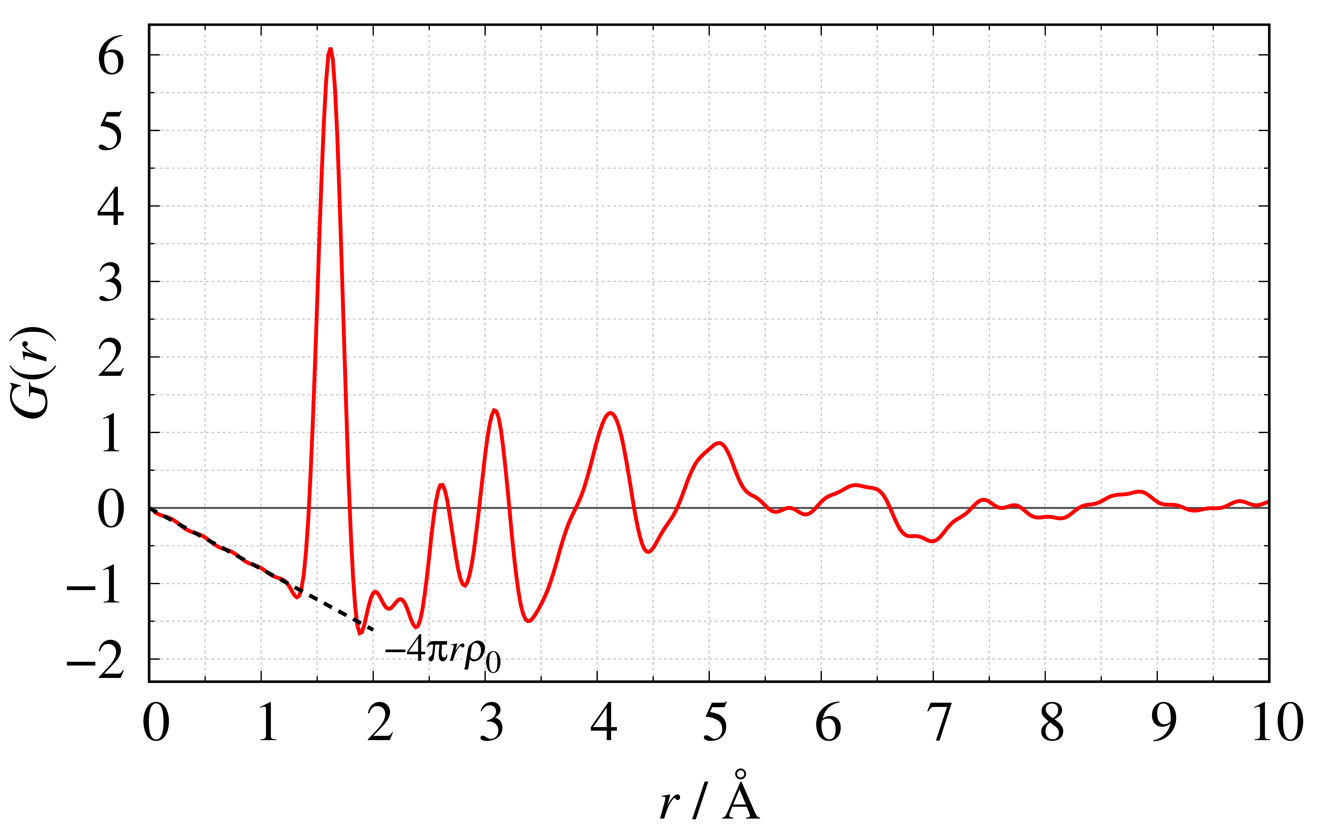
Atomic Pair Distribution Function $g(r)$
\begin{equation} g(r) = \frac{1}{2\pi^2\rho_{0}r} \int^{Q_{\max}}_{Q_{\min}} {Q\{S(Q)-1\}\sin Qr} \,\mathrm{d}Q + 1\nonumber \end{equation}

Radial Distribution Function RDF $R(r)$
\begin{equation} R(r) = \frac{2r}{\pi} \int^{Q_{\max}}_{Q_{\min}} {Q\{S(Q)-1\}\sin Qr} \,\mathrm{d}Q + 4\pi r^2\rho_{0}\nonumber \end{equation}

Total Correlation Function $T(r)$
\begin{equation} T(r) = \frac{2}{\pi} \int^{Q_{\max}}_{Q_{\min}} {Q\{S(Q)-1\}\sin Qr} \,\mathrm{d}Q + 4\pi r\rho_{0}\nonumber \end{equation}

PDF analysis often uses $g(r)$ for amorphous and $G(r)$ for crystalline. They can also be easily converted to each other.
References:
[1] Y.Shiramata and M.Yoshimoto, Rigaku Journal, 50(1), (2019) 1-8.[2] D. A. Keen. J. Appl. Cryst., 34, (2001), 172. doi: 10.1107/S0021889800019993.
Basic information about RMC modeling
The Reverse Monte-Carlo (RMC) method, reported by R. L. Mcgreevy and L. Putzai, is a method for probing structural model which is consistent with the observed S(Q) and G(r). It was initially commonly used as a method for probing the structure of liquids and amorphous materials ¹. However, RMC methods have been widely used for local structure analysis of crystalline materials due to developing the RMCPOW simulation ² by A. Mellergård and R. L. Mcgreevy and the RMCProfile simulation ³ by M. G. Tucker et al.
PDFFIT ⁴ and PDFgui ⁵ are widely known as PDF analysis tools for crystalline materials, and they are called "Small Box Simulations" because they use a unit cell to reproduce the measured G(r). On the other hand, RMC is called a "Large Box Simulation" because it requires a large computational box to reproduce actual measurements. The RMC method provides real space information as follows: revised structure mode, partial correlation, angular histogram.
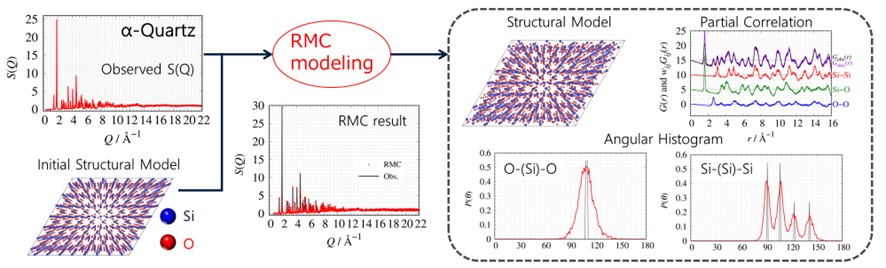
Outline of structure modelling by RMC
The flow of RMC modelling
There are two important equations to understand the RMC modelling. At first, the scattering intensity is calculated from the atomic coordination as follows:
\begin{equation} S_{\mathrm{RMC}}(Q) = \rho_0 \displaystyle \int_{0}^{r_{\mathrm{max}}} 4πr^2 (g_{\mathrm{RMC}} (r)-1) \frac{{\mathit{\sin{Qr}}}}{\mathit{Qr}} \mathit{dr}\end{equation}
where $\rho_{0} = N/V$ is the number density (N: the number of atoms (particles) in the calculation box), $r_{\max}$ is the maximum distance in RMC modelling, and $Q$ is the scattering vector.
The estimated structure is evaluated the comparison between an observed value and calculated value using a standard χ² test as follows:
\begin{equation} x^2 = \displaystyle \sum_{i=1}^{N} \frac{(S_{\mathrm{obs}}(Q_i)- S_{\mathrm{RMC}}(Q_i))^{2}}{\sigma^{2}(Q_i)} \end{equation}
where $S_{obs} (Q_i )$ is the observed value, $S_{RMC} (Q_i )$ is the calculated value and $σ^2 (Q_i )$ is the experimental error.
The RMC trials are generated by random numbers.
- Select the atom and the movement trials were generated by random number.
- If the calculated value (S(Q) or G(r)) from the atomic coordination after the move has a χ² value of the measured value,
- Small: Accept the trial 1
- Large: Reject the trial 1
- Repeat steps 1 and 2 until the χ² value falls below the target value.
Actual RMC calculation
Changes in S(Q) and G(r) during RMC modelling
References:
[1] R.L. McGreevy, L. Pusztai, Molec. Simul. 1 (1988) 359-367. doi: 10.1080/08927028808080958 [2] A. Mellergård ,R. L. McGreevy, Acta Crystallogr. A 55 (1999) 783-789. doi: 10.1107/S0108767399000197 [3] M.G. Tucker, D.A. Keen, M.T. Dove, A.L. Goodwin, Q. Hui, J. Phys.: Condens. Matter. 19 (2007) 335218. doi: 10.1088/0953-8984/19/33/335218 [4] Th. Proffen, S.J.L. Billinge, J. Appl. Crystallogr. 32 (1999) 572-575. doi: 10.1107/S0021889899003532 [5] C.L. Farrow, P. Juhas, J.W. Liu, D. Bryndin, E.S. Božin, J. Bloch, T. Proffen, S.J.L. Billinge, J. Phys.: Condens. Matter. 19 (2007) 335219. doi: 10.1088/0953-8984/19/33/335219.Measurement for PDF analysis
The measurement for PDF analysis is called a Total Scattering Measurement because it uses not only diffraction peaks but also broad scattering intensity arising from the local structure (diffuse scattering), which is treated as background in powder XRD measurement, for analysis.
Data from total scattering measurements must be devised in such a way that extra scattering intensity from the instrument (parasitic scattering) is not included.
Total scattering intensity is only required the information from the sample and container (or air scattering intensity) but is best to exclude any of the following components: parasitic scattering from the instrument, the background contamination due to X-ray fluorescence, etc.
In addition, there are three points to be considered for data acquisition.
1) X-ray wavelengths
The scattering vector is defined according to the following equation, which means that the shorter incident X-ray wavelengths (i.e., higher energy X-rays) can measure the total scattering data with the widest $Q$ -range.
\begin{equation} Q = \frac{4\pi}{\lambda} \sin \theta \nonumber \end{equation}
In laboratories, $\mathrm{Mo\ K}\alpha$ and $\mathrm{Ag\ K}\alpha$ raditions are often used for the total scattering measurement.
SiO₂ glass samples measured with $\mathrm{Cu\ K}\alpha$, $\mathrm{Mo\ K}\alpha$, and $\mathrm{Ag\ K}\alpha$ radiations are shown with $2\theta$ on the horizontal axis (left figure) and $Q$ on the horizontal axis (right figure). The three profiles feature the same measurement $2\theta$ angles. $\mathrm{Mo\ K}\alpha$ and $\mathrm{Ag\ K}\alpha$ radiations can measure total scattering intensity with a wider Q range than that of $\mathrm{Cu\ K}\alpha$ radiation.


Figure 4. Profiles of SiO₂ glass measured at various wavelengths (left: horizontal axis $2\theta$; right: horizontal axis Q)
So, what is the benefit of measuring total scattering intensity with a wide $Q$ range?
$G(r)$ obtained from the Fourier transform of $S(Q)$ has a finite peak width that is unrelated to the structural disorder, caused by a termination error arising from the measurable maximum $Q$ value $Q_{\max}$ and it can be easily estimated using the direct-resolution $\Delta r$ defined as follows:
\begin{equation} \Delta r = \frac{\pi}{Q_{\max}} \nonumber \end{equation}
In the case of X-rays, the condition $2\theta=180^{\circ}$ can be used to estimate a convenient $\Delta r$, which is ¼ of the wavelength of the X-rays used in the measurement.
\begin{equation} \Delta r \approx \frac{\lambda}{4} \nonumber \end{equation}
Figure. 4 shows the RDF of SiO₂ glass for each X-ray wavelength.
Si-O correlations are observed at all wavelengths. Although the RDFs of $\mathrm{Mo\ K}\alpha$ and $\mathrm{Ag\ K}\alpha$ radiations can detect the two distinct peaks related to O-O and Si-Si correlation, with Cu Kα radiation the two peaks are originally observed as a single peak because the real-spatial resolution is lower (i.e., larger $\Delta r$ value). These results indicate that the shorter-wavelength $\mathrm{Mo\ K}\alpha$ and $\mathrm{Ag\ K}\alpha$ radiations are recommended for laboratory equipment.
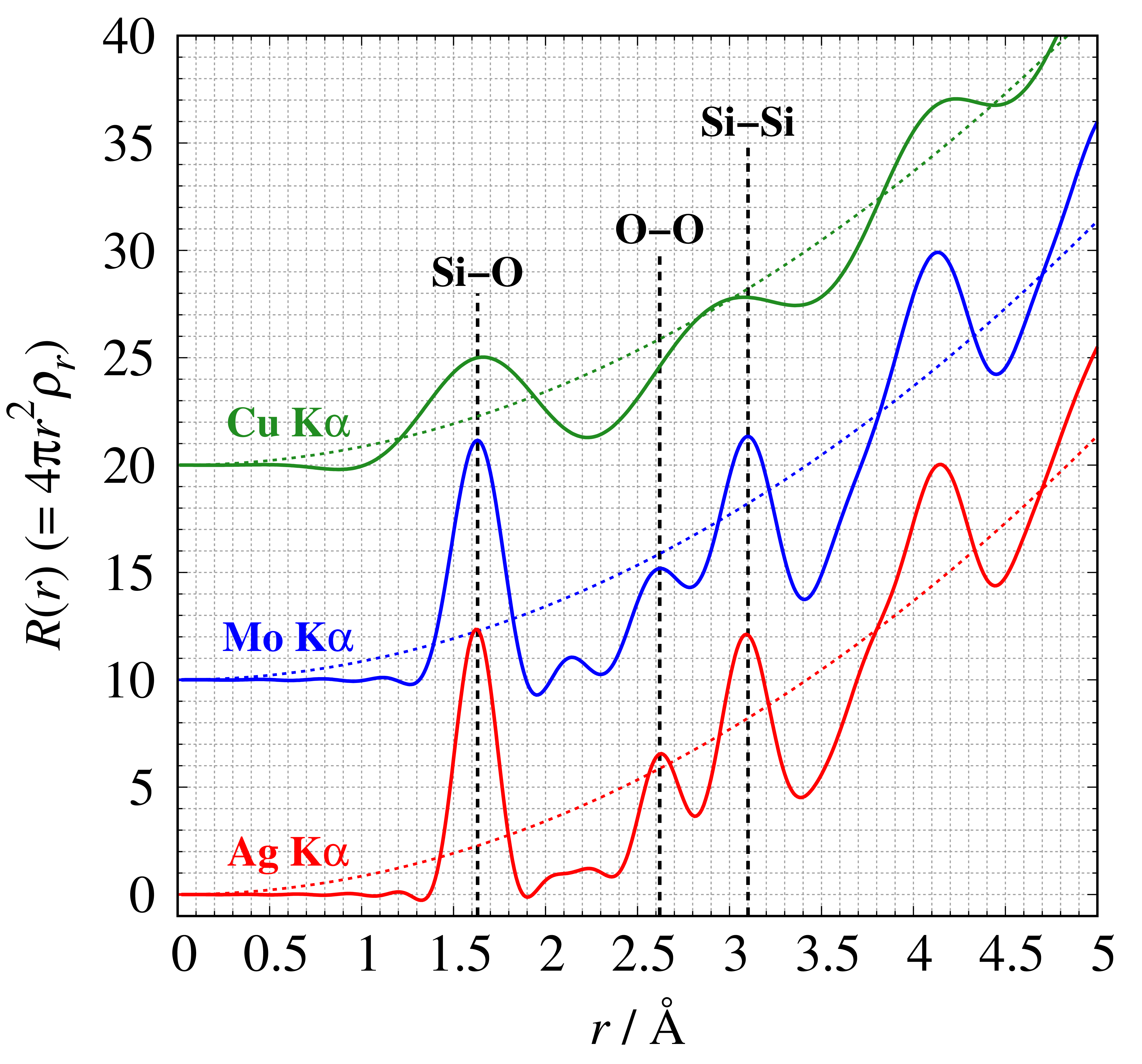
Figure 5. Radial distribution function $R(r)$ measured at each wavelength
Next, we would like to consider which wavelength should be selected, $\mathrm{Mo\ K}\alpha$ or $\mathrm{Ag\ K}\alpha$ radiation.
As mentioned previously, one might think that the $\mathrm{Ag\ K}\alpha$ line, with its higher real-space resolution $\Delta r$, would be better for total scattering measurements. However, depending on the sample to be measured, X-ray fluorescence from the sample may occur, making analysis difficult. Figure 6 shows the compatible wavelengths for the elements of note.

Figure 6. Wavelengths of X-rays compatible with each element
Figure 7 shows the total scattering profiles of ZrO₂ measured using $\mathrm{Mo\ K}\alpha$ and $\mathrm{Ag\ K}\alpha$ radiation. Although the total scattering profiles using $\mathrm{Mo\ K}\alpha$ radiation shows high S/N with a low background, that using $\mathrm{Ag\ K}\alpha$ radiation shows low S/N (shows small diffracted peaks) due to the background contamination of X-ray fluorescence.

Figure 7. Total scattering profiles of ZrO₂ measured with $\mathrm {Ag\ K}\alpha$ (blue) $\mathrm{Mo\ K}\alpha$ (red)
Therefore, $\mathrm{Mo\ K}\alpha$ radiation is the appropriate X-ray source for total scattering measurements if samples contain a small amount of ZrO₂, which is often used as a material for ball milling. To reduce the background contamination from X-ray fluorescence, the narrow detector's discriminator window cannot fully perform a total scattering measurement because the detector setting only partially measures Compton scattering.
2) Measurement method (reflection or transmission) and absorption correction
There are two measurement methods: transmission (e.g., Debye Scherrer geometry) and reflection (e.g., Bragg-Brentano geometry). The transmission method is often used, and the sample is often filled into a capillary. In such cases, the empty capillary profile is used as background data and must be subtracted from the data for the sample sealed in the capillary. In the case of the reflection method using $\mathrm{Mo\ K}\alpha$ or $\mathrm{Ag\ K}\alpha$, be careful not to observe scattering from the sample plate due to the deeper penetration depth of the sample. In addition, absorption of X-rays by the sample cannot be avoided in either method. The PDF plug in supports absorption correction in cylindrical transmission, symmetric plate transmission, and symmetric plate reflection (Figure 8).
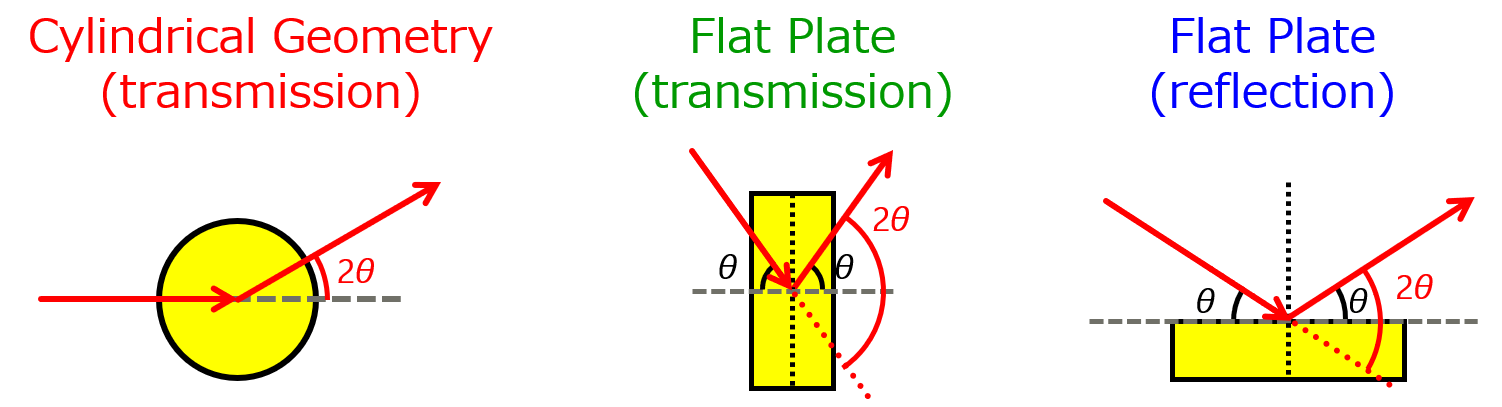
Figure 8. Schematic diagram of the measurement method
3) Measurement condition (Intensity)
Among the measurement conditions that can be set by the user, the parameters that vary in intensity are the scanning speed and sampling interval. The figures below show 2θ profiles and PDF profiles of SiO₂ glass with varying intensity at different scanning speeds. The intensity of the peak tops is shown in the left figure, and the PDF on the right corresponding to that color shows that the lower the intensity, the more noise has been included. Therefore, it is necessary to devise ways to obtain high intensity, and instrument-dependent parameters such as the X-ray source and detector are also important.


Figure 9. Measured 2θ profile (left) and PDF profile (right)
Introduction of SmartLab
We would like to introduce the features of SmartLab (goniometer) as an instrument for total scattering measurement. The goniometer is equipped with an X-ray source, a multi-layer mirror for monochromatizating incident X-rays, a sample stage, and a detector, excluding the slits.
Goniometer
The measurement angle can operate up to $160^{\circ}$ in $2\theta$ with the incident angle fixed at $0^{\circ}$ (see figure below). SmartLab provides high angular resolution because the goniometer radius is 300 mm.

Figure 10: Inside of SmartLab (left, $2\theta=160^{\circ}$ placement), capillary installation (right, movie)
X-ray source
Sealed tube and rotating cathode tube can be selected, and their respective outputs are summarized in the table below. Rotating cathode fluorescent tubes are the highest-output tubes among laboratory equipment.
Table. Output of each target
| Wavelength | Output(kW) (Sealed tube) |
Output(kW) (Rotating anode tube) |
| $\mathrm{Mo\ K}\alpha$ | 3.0 kW (60 kV-50 mA) |
9.0 kW (60 kV-150 mA) |
| $\mathrm{Ag\ K}\alpha$ | 2.16 kW (60 kV-36 mA) |
6.0 kW (60 kV-100 mA) |
Multilayer mirror
The use of a CBO-E with multilayer mirrors makes it possible to focus the X-ray beam onto the detector, making it possible to acquire high-intensity, high-resolution data using the transmission method.
Sample stage
A capillary attachment for the transmission method allows easy mounting of the sample. Figure. 10 shows the procedure for mounting the capillary on the attachment as a movie. You can easily set up the sample for total scattering measurement.
Detector
The total scattering measurement requires a detector with high-efficiency detection for high-energy X-rays. Therefore, Rigaku offers D/teX Ultra250 HE and HyPix-3000 HE equipped with a thicker Si sensor compared with the detectors for ${\mathrm {Cu\ K}}\alpha$ radiation. Although detectors equipped with CdTe sensors are often recommended for PDF analysis, note that, for example, the absorption rate of ${\mathrm {Mo\ K}}\alpha$ and ${\mathrm {Ag\ K}}\alpha$ at high-energy wavelengths is 100%, but the detection efficiency of X-rays is not 100%, and the detection efficiency at low-energy wavelengths, such as ${\mathrm {Cu\ K}}\alpha$, is significantly reduced.
Data Comparison between SmartLab and Synchrotron
The structure factor $S(Q)$ measured with a SmartLab and at a synchrotron radiation facility (SPring-8, BL04B2) are shown in Figure 11. Good agreement between the two shows that the total scattering pattern measured with SmartLab is comparable to that at a synchrotron. In addition, if you purchase the PDF analysis option, we calibrate the instrument status for the total scattering measurement for each customer. Therefore, you can measure and analyze without troublesome settings.

Figure 11. Comparison of structure factor $S(Q)$ of SiO₂ glass measured with SmartLab and at BL04B2 (SPring-8)
SmartLab Studio $\mathrm{I\hspace{-.01em}I}$
SmartLab Studio $\mathrm{I\hspace{-.01em}I}$ (SLSII) is an integrated software package for X-ray analysis from measurement to analysis.
In this section, we will introduce the Measurement plug-in for measurement and the PDF plug-in for analysis.
Measurement plug-in
For a total scattering measurement, mirror adjustment, optical system adjustment, capillary center position adjustment, and profile measurement with dedicated detector energy mode are realized, and anyone can easily execute from adjustment to measurement.

Figure 12. Description of element replacement at the time of optical system adjustment
PDF plugin
The complex PDF analysis procedure can be represented as a flow diagram and analyzed step by step.
In this section, we will introduce the $S(Q)$ calculation, PDF calculation, and RMC modeling.
$S(Q)$ calculation
When calculating $S(Q)$, the sum of the Compton scattering and atomic scattering components is displayed to confirm that the interferential scattering intensity from the sample has been correctly extracted.

Figure 13. The $S(Q)$ tab on PDF plug-in.
Figure 14 shows an example of how the intensity-corrected profile (red) matches the atomic scattering factor (black). If they match, the curve of the atomic scattering factor runs through the center of the intensity-corrected profile, and the calculated $S(Q)$ profile (green) oscillates periodically around 1 on the second vertical axis (Figure 14 left). However, if they do not match, the $S(Q)$ profiles are rightward sloping, which implies that the atomic number ratios and absorption calculations for the sample are incorrect (Figure 14 right).
The PDF plug-in also makes it easy to determine if the analysis is good or bad in this way. By the way, baseline correction of $S(Q)$ distortion by polynomial approximation has also been reported, but it should be noted that it may cause loss of true information on the short side.

Figure 14. $S(Q)$ Good or bad calculation Left: Good analysis example; Right: Bad analysis example
PDF calculation
The PDF calculation screen is shown below. If there is crystal structure information, etc., the bond distance is automatically calculated and overlaid on the profile with a blue line. Peak positions are also searched, making it easy to obtain peak position information. Of course, $g(r)$, $G(r)$, $R(r)$ and $T(r)$ are all supported and can be converted to each other with a single click.

Figure 15. $G(r)$ Calculation screen
Unlike the $S(Q)$ correction by polynomial approximation, SLS$\mathrm{I\hspace{-.01em}I}$ has a ripple rejection function. The figure shows their effects in $G(r)$. The window function has the effect of suppressing oscillations due to Fourier transform truncation errors. The ripple rejection correction removes non-physical vibration components below the coupling distance set by the PDF plug-in's feature correction from $S(Q)$ and, thus, extra vibration can be calculated without including the extra vibration in $G(r)$. This allows the fitting accuracy of the structure estimation by $G(r)$ to be improved.
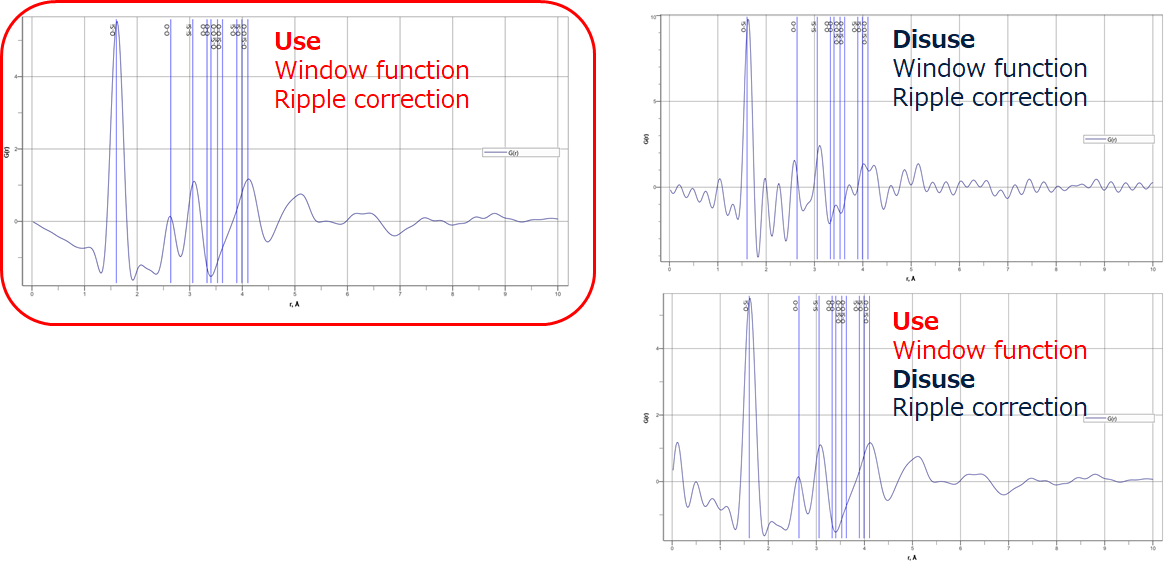
Figure 16. $G(r)$ with window function and ripple correction applied
RMC calculation
Although RMCProfile is a well-known program for the RMC method, we have also implemented RMC functionality in the PDF plug-in. Currently, the RMC implemented in the PDF plug-in supports the estimation of local structures in crystal structures. With conventional RMC, it is difficult to set parameters, and it takes a lot of time to learn how to use RMC. However, RMC implemented in the PDF plug-in automatically sets parameters, so RMC can be run with only the minimum necessary parameters.

Figure 17. RMC calculation
Density Determination from Total Scattering Data
It is well known that the density of a sample is calculated from the slope of $G(r)$ in the region less than the nearest neighbor distance. The obtained $G(r)$ is, however, often affected by non-physical modulation of the experimentally observed $S(Q)$ and does not show a linear slope in the less-than-nearest-neighbor region; therefore, the estimated density has a large uncertainty. To overcome the problem, we have developed a $Q$-space iteration formula to remove such unphysical modulation of the experimentally observed $S(Q)$, without introducing any ambiguous parameters.
First, we demonstrate the determination of the density of $\mathrm{SiO_{2}}$ glass from total scattering profile. Figure 18 shows the estimated density $\large{\rho}_{0}$ of $\mathrm{SiO_{2}}$ glass and the corresponding goodness of fit $R$ for each iteration. The estimated atomic-number density converges to $\large{\rho}_{0}$$= 0.06311 \mathrm{\ atoms}\cdot Å^{-3}$ as the number of iterations increases and the $R$ value gradually decreases for each iteration step. Finally, we obtain the atomic-scale number density ($\raise{.7ex}\hbox{$\rho$}_{0} = 0.06311 \mathrm{\ \ atoms}\cdot Å^{-3}$) of $\mathrm{SiO_{2}}$ glass, which is consistent with the reported bulk density 1, 2) ($(\raise{.7ex}\hbox{$\rho$}_{\mathrm{bulk}} = 0.06613 \mathrm{\ atoms}\cdot Å^{-3})$) within $5 \%$.


Fig. 18 The estimated density and the corresponding goodness of fit $R$ of $\mathrm{SiO_{2}}$ glass for each iteration.
Next, we estimated the atomic number density of crystalline Ni by the same procedure. The determined Ni density $\raise{.7ex}\hbox{$\rho$}_{0}=0.09148 \mathrm{\ atoms}\cdot Å^{-3}$ is consistent with the bulk density $\raise{.7ex}\hbox{$\rho$}_{\mathrm{bulk}}=0.09132 \mathrm{\ atoms}\cdot Å^{-3}$ calculated from the lattice parameter (space group: $F\bar{d}3m$, $a = 3.52503 Å$), within $1\%$. Figure 19 shows the comparison between before and after density estimation of $S(Q)$ and $G(r)$ and they change little during the procedures.


Figure 19. The comparison of (left) $S(Q)$ and (right) associated $G(r)$ of crystalline Ni before and after the determination density.
The proposed method can be applied to various samples where it is difficult to measure the density by Archimedes' principle (e.g., porous material, water-reactive substances). Please refer to this article 1) if you want more detailed information about atomic-number density determination of a sample from total scattering data.
References:
[1] M. Yoshimoto, K. Omote, J. Phys. Soc. Jpn. 91 (2022) 104602 (7pp). doi: 10.7566/JPSJ.91.104602[2] M.Yoshimoto, Rigaku Journal 53 (2022) 27-36.
Local distortion analysis of $\mathrm{LiMn_{2}O_{4}}$ LMO by the RMC method
The spinel $\mathrm{LiMn_{2}O_{4}}$ (LMO) is a cathode material candidate and has a structural phase transition with a hysteresis between the heating and the cooling process 1, 2). In the high-temperature phase, LMO forms a cubic structure in space group $F\bar{d}3m$. There is a unique $\mathrm{MnO_{6}}$ octahedron in cubic LMO. For the low-temperature phase, LMO forms an orthrhombic structure that is a $3a \times 3a \times 1a$ superstructure based on cubic LMO and $\mathrm{MnO_{6}}$ octahedra are distorted and separated into five types. We will present an example of local structure analysis of LMOs with these unique features by the RMC method.


Figure 20. The structural model of LMO;
(left) high-temperature phase (cubic model) and (right) low-temperature phase (orthorhombic model)
Figure 21 shows the comparison of $S(Q)$ between calculated and observed. The bottom of Fig. 21 also shows the corresponding residual curve. We have successfully constructed LMO structural models consistent with the experimental $S_{\mathrm{obs}}(Q)$ by RMC modeling.
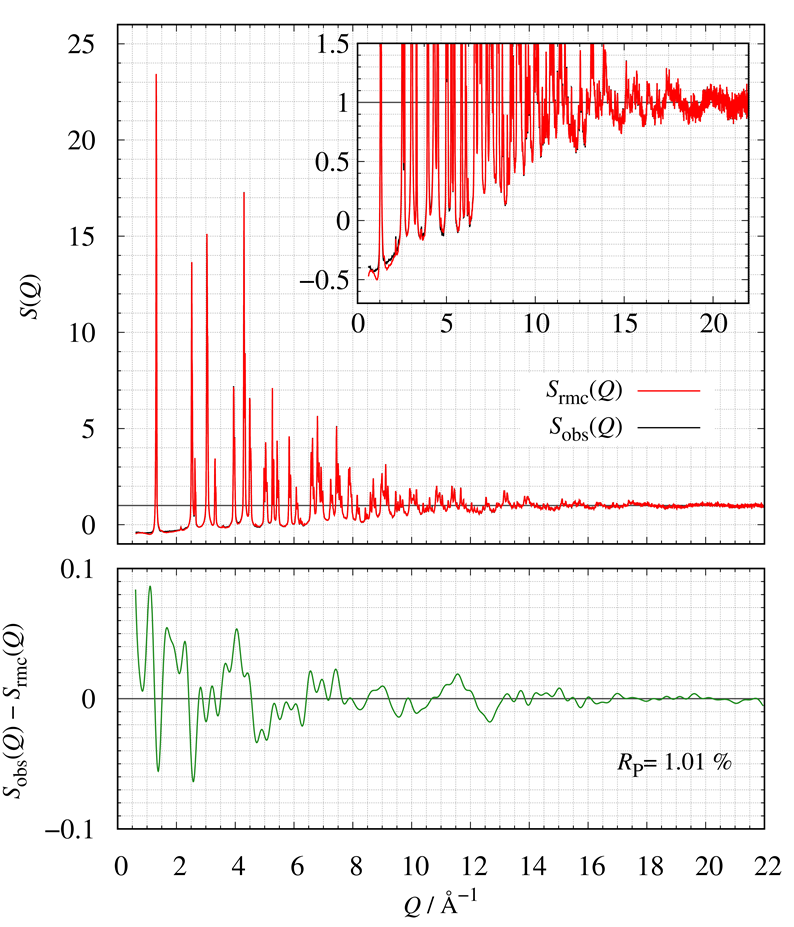
Figure 21. The comparison of $S(Q)$; (red) calculated and (blue) obtained.
To evaluate the local structure of $\mathrm{MnO_{6}}$ octahedra, the bond valence sum BVS method is applied to the structural model estimated by the RMC method to calculate the valence of each Mn site (BVS parameter: $r_0 = 1.753 Å$, $R=0.37 Å$). Most Mn sites are classfied $\mathrm{Mn^{3+}:\ 58.98\ \%}$ and $\mathrm{Mn^{4+}:\ 34.96\ \%}$. The correlation related to $\mathrm{Mn^{2+}}$ and $\mathrm{Mn^{5+}} $ are not used for detailed discussion of $\mathrm{MnO_{6}}$ octahedra because those percentages ($\mathrm{Mn^{2+}}:\ 5.95\%$, $\mathrm{Mn^{5+}}:\ 0.097 \%$) are low.
Figure 22 shows the O-(Mn)-O angular histogram of $\mathrm{Mn^{3+}}$ and $\mathrm{Mn^{4+}}$. The angular histogram of the ideal octahedron has two peaks at $\theta = 90^{\circ}$ and $180^{\circ}$ but the simulated $\mathrm{Mn^{3+}}$ angular histogram (blue) shows a peak at less than $\theta = 90^{\circ}$ with wider distribution than that of $\mathrm{Mn^{4+}}$ (red). Please refer the article 3,4) if you want more information about this study and the RMC method.

Figure 22. The O-(Mn)-O angular histogram of $\mathrm{Mn^{3+}}$ and $\mathrm{Mn^{4+}}$.
The RMC method can provide local structural information in polycrystalline samples.
References:
[1] J. Rodríguez-Carvajal, G. Rousse, C. Masquelier, M. Hervieu, Phys. Rev. Lett. 81 (1998) 4660-4663. doi: 10.1103/PhysRevLett.81.4660[2] G. Rousse, C. Masquelier, J. Rodríguez-Carvajal, E. Elkaim, J.-P. Lauriat, J.L. Martínez, Chem. Mater. 11 (1999) 3629-3635. doi: 10.1021/cm9910963
[3] M. Yoshimoto, K. Omote, Appl. Phys. Express 16 (2023) 015005 (4pp). doi: 10.35848/1882-0786/acb2b0
[4] M.Yoshimoto, Rigaku Journal, 53 (2022) 27-36.
Analysis of local structural changes during Li₃PS₄ crystallization
Li₃PS₄, a solid sulfide electrolyte, is widely known to show multiple phases such as glass α, β and γ phases. The characteristics of the three phases are shown in the figure.
In this application, the total scattering measurement is performed through to R.T.~250℃ and the local structural changes during crystallization are visualized by the RMC method.
The following figure shows the comparison between the observed G(r) with crystallization and the weighted partial pair correlation $w_{ij}G_{ij} (r)$ in the crystalline state (T = 250°C, t = 75.5 h). The shoulders and peaks at r ≥ 4.5 Å indicate P-S correlation and S-S correlation, respectively. Thus, the weighted partial correlations (i.e., $w_{ij}G_{ij} (r)$) can describe the profile changes in the observed G(r) with crystallization.

The comparison between $G(r)$ and $w_{ij}G_{ij} (r)$
top: $G(r)$ of each measurement time, bottom: $w_{ij}G_{ij} (r)$ of P-S, S-S, and S-Li
RMC refined atomic coordination collapsed into a gamma Li₃PS₄ unit cell of each state as shown in the figure below. As a general tendency, the average atomic distribution is narrow, with structural changes from glass to crystal. Furthermore, by analyzing more detail, it can be found that the average atomic distribution of high temperature glass becomes slightly broader than that of glass at room temperature.
The tendency of the analysis result on the atomic distribution in the unit cell is consistent with the Li ionic conductivity result with crystallization in previous study ². This study shows that the libration of PS₄ anions plays an important role in Li ion migration in solid sulfide electrolytes.

The distribution of each atom in the unit cell at each measurement temperature
Full details of this application are published in Ref 3
References:
[1] K. Homma, M. Yonemura, T. Kobayashi, M. Nagao, M. Hirayama, R. Kanno, Solid State Ionics, 182 (2011) 53–58. doi: 10.1016/j.ssi.2010.10.001 [2] S. Shiotani, K. Ohara, H. Tsukasaki, S. Mori, R. Kanno, Sci. Rep. 7 (2017) 6972 (7pp). doi: 10.1038/s41598-017-07086-y [3] M. Yoshimoto, T. Kimura, A. Sakuda, C. Hotehama, Y. Shiramata, A. Hayashi, K. Omote, Solid State Ionics, 401 (2023), 116361 (8pp). doi: 10.1016/j.ssi.2023.116361Questions about PDF Analysis
Some of the questions we have received from customers are listed below.
Q1. For lab instrument-based PDF analysis, should I monochromatize the $\mathrm{K\alpha}$ radiation to $\mathrm{K\alpha_{1}}$ radiation?
A. No, it is not necessary to monochromatize. The reason is that the real space resolution $\Delta r$ is calculated to be only 0.001 Å or less between the monochromatized $\mathrm{K\alpha_{1}}$ radiation and the general $\mathrm{K\alpha_{1}}$ radiation data. Furthermore, monochromatizing to $\mathrm{K\alpha_{1}}$ results in 1/10 of the intensity before monochromatization; therefore, measurement time takes 10 times longer.
Table. $\Delta\ r$ at each wavelength
| Characteristic X-ray | $\lambda\ (Å)$ | $Q\ (Å^{-1})$ | $\Delta r$ (Å) |
| $\mathrm{Ag\ K\alpha}$ | 0.560880 | 22.0644 | 0.1428 |
| $\mathrm{Ag\ K\alpha_{1}}$ | 0.559422 | 22.1219 | 0.1420 |
| $\mathrm{Ag\ K\alpha_{2}}$ | 0563813 | 21.9496 | 0.1431 |
Q2. Can I perform PDF analysis of thin film samples?
A. It is currently difficult with a lab machine because Mo and Ag wavelengths have deeper penetration depth, so information from substrates other than thin films will be introduced.
Q3. Can I perform PDF analysis of compounds?
A. Yes; however, the weight ratio or composition ratio may make it difficult to see the desired interatomic distance. Also, when fitting with PDFgui, the weight ratio can be obtained from the scale factor.
Q4. How long does it take to analyze a PDF?
A. A test measurement takes from a few minutes to 10 minutes. Full-scale measurement often takes about 4 hours. Full-scale modeling analysis may take up to a day. The measurement time will increase or decrease depending on the analysis and quality desired.
Q5. Are detectors equipped with CdTe sensors suitable for PDF analysis?
A. CdTe detectors certainly have good absorption at high-energy wavelengths, but their detection efficiency is not 100%. In the case of low-energy X-rays such as $\mathrm{Cu\ K}\alpha$, a detector equipped with CdTe sensors will hav lower detection efficiency, and another detector is required. Furthermore, commercially available detectors equipped with CdTe sensors require greater maintenance compared to Si sensors, because of a water-cooling system for device temperature control and a dry air circulation system for keeping dry condition.
Q6. Can the reflection method be used for analysis?
A. The reflection method can also be used for analysis, but it is a little difficult to estimate the amount of BG components such as air scattering in the measured total scattering data. Therefore, we generally recommend the transmission method.
Q7. Is it possible to calculate the partial correlations from the observed data of a multi-element system?
A. Yes, the partial correlations can be calculated by common modeling tools.
Q8. What are the advantages and disadvantages of EXAFS (Extended X-ray Absorption Fine Structure) and PDF?
A. The advantage of XAFS is its element selectivity.
Therefore, it is possible to directly observe relatively short-range information about the first and second neighbors of correlations that include the element of interest.
The disadvantages of EXAFS are the unreliability of data on the long-range side and the need for phase correction to obtain absolute distances. On the other hand, the advantage of PDF is that it can capture all information from short to long distances, allowing structural analysis.
The disadvantage of PDF is that correlations are observed for all atoms in the system, especially since most real materials are composed of multiple elements and it is impossible to extract specific correlations only from the measured values.
Table. Comparizon between PDF and EXAFS
| EXAFS | ||
| Element selectivity | No | Yes |
| Distance information | Obtained without correction | Phase correction is required |
| Obtained distance information | Weighted correlation for all elements | Correlation for specific elements |
Q9. Can I use SmartLab Studio $\mathrm{I\hspace{-.01em}I}$?
A. Yes, it is possible. The data can be analyzed by providing wavelength information and horizontal polarization ratio to the measured data.
Q10. In the case of a mixture of amorphous and crystalline, is it possible to extract structural information from each?
A. Since diffraction from amorphous is much weaker in intensity than from crystalline materials, information from amorphous materials is likely to be buried by information from crystals, making extraction difficult.
Q11. Can we observe Li-Li correlations in Li₂S?
A. As it turns out, Li-Li correlations do not appear in total scattering data or PDF analysis results.
TT. E. Faber and J. M. Ziman reported the idea of classifying total correlations calculated by Debye's scattering formula by correlation (partial correlation)₁)。
The structure factors and PDFs expressed in this approach are called Faber-Ziman type structure factors and PDFs.
Here, Faber-Ziman type structure factors are explained using Li₂S as an example.
\begin{equation} S(Q) = \frac{c_{\mathrm{Li}}f_{\mathrm{Li}}c_{\mathrm{Li}}f_{\mathrm{Li}}}{\langle f \rangle^{2}}S_{\mathrm{LiLi}}(Q) + \frac{c_{\mathrm{Li}}f_{\mathrm{Li}}c_{\mathrm{S}}f_{\mathrm{S}}}{\langle f \rangle^{2}}S_{\mathrm{LiS}}(Q) + \frac{c_{\mathrm{S}}f_{\mathrm{S}}c_{\mathrm{Li}}f_{\mathrm{Li}}}{\langle f \rangle^{2}}S_{\mathrm{SLi}}(Q) + \frac{c_{\mathrm{S}}f_{\mathrm{S}}c_{\mathrm{S}}f_{\mathrm{S}}}{\langle f \rangle^{2}}S_{\mathrm{SS}}(Q) \nonumber \end{equation} \begin{equation} \langle f \rangle = \sum_{i}^{n}c_if_i \nonumber \end{equation}
$S(Q)$ is the structure factor of $\mathrm{Li_{2}S}$, and $c_{i}$ and $f_{i}$ are the concentration of $i$ atoms and the atomic scattering factor, respectively.
Furthermore, Li-O and O-Li in the equation are equivalent (indistinguishable) and can be combined into one.
\begin{equation} S(Q) = \frac{c_{\mathrm{Li}}f_{\mathrm{Li}}c_{\mathrm{Li}}f_{\mathrm{Li}}}{\langle f \rangle^{2}}S_{\mathrm{LiLi}}(Q) + \frac{2c_{\mathrm{Li}}f_{\mathrm{Li}}c_{\mathrm{S}}f_{\mathrm{S}}}{\langle f \rangle^{2}}S_{\mathrm{LiS}}(Q) + \frac{c_{\mathrm{S}}f_{\mathrm{S}}c_{\mathrm{S}}f_{\mathrm{S}}}{\langle f \rangle^{2}}S_{\mathrm{SS}}(Q) \nonumber \end{equation}
From this equation, we see that the correlation observed in the total scattering intensity is the sum of partial correlations with the atomic concentration and atomic scattering factor as coefficients. Since the structure factor $S(Q)$ and the PDF $G(r)$ can be interconverted by the Fourier transform, the Faber-Ziman type structure factor concept can also be applied to $G(r)$. However, for $G(r)$, the atomic scattering factor $f$ is the atomic number $Z$.
\begin{equation} G(r) = \frac{c_{\mathrm{Li}}Z_{\mathrm{Li}}c_{\mathrm{Li}}Z_{\mathrm{Li}}}{\langle Z \rangle^{2}}G_{\mathrm{LiLi}}(r) + \frac{2c_{\mathrm{Li}}Z_{\mathrm{Li}}c_{\mathrm{S}}Z_{\mathrm{S}}}{\langle Z \rangle^{2}}G_{\mathrm{LiS}}(r) + \frac{c_{\mathrm{S}}Z_{\mathrm{S}}c_{\mathrm{S}}Z_{\mathrm{S}}}{\langle Z \rangle^{2}}G_{\mathrm{SS}}(r) \nonumber \end{equation} \begin{equation} \langle Z \rangle = \sum_{i}^{n}c_iZ_i \nonumber \end{equation}
The table summarizes the coefficients of the Faber-Ziman type structure factor for the partial correlation of $\mathrm{Li_{2}S}$.
Since Li-Li only accounts for about 7% of the total, we can see that it is likely to be difficult to observe peaks of only Li-Li correlations in the actual $G(r)$.
Table Faber-Ziman coeficient of Li₂S in $G(r)$
| Correlation | Li-Li | Li-S | S-S |
| Coefficient % | 7.44 | 39.67 | 52.89 |
Finally, the Faber-Ziman type structure factor and the general form of the PDF are included.
In the case of $S(Q)$
\begin{equation} S(Q)=\sum_{i, j\ge i}(2-\delta_{ij})\frac{c_{i}f_{i}c_{j}f_{j}}{\langle f \rangle} S_{ij}(Q) \nonumber \end{equation}
In canse of $G(r)$
\begin{equation} G(r)=\sum_{i, j\ge i}(2-\delta_{ij})\frac{c_{i}Z_{i}c_{j}Z_{j}}{\langle Z \rangle} G_{ij}(r) \nonumber \end{equation}
$\delta_{ij}$ is Kronecker's delta. Thus the correlation for homologous atoms is$(c_{i}f_{i}c_{j}f_{j})/\langle f \rangle$ and between dissimilar atoms is $(2c_{i}f_{i}c_{j}f_{j})/\langle f \rangle$.
References:
[1] T. E. Faber and J. M. Ziman, Phil. Mag., 11(1965), 153-173. (https://doi.org/10.1080/14786436508211931)Structural models drawn using VESTA, K. Momma and F. Izumi, J. Appl. Crystallogr. , 44(2011) 1272-1276. (doi:10.1107/S0021889811038970)

